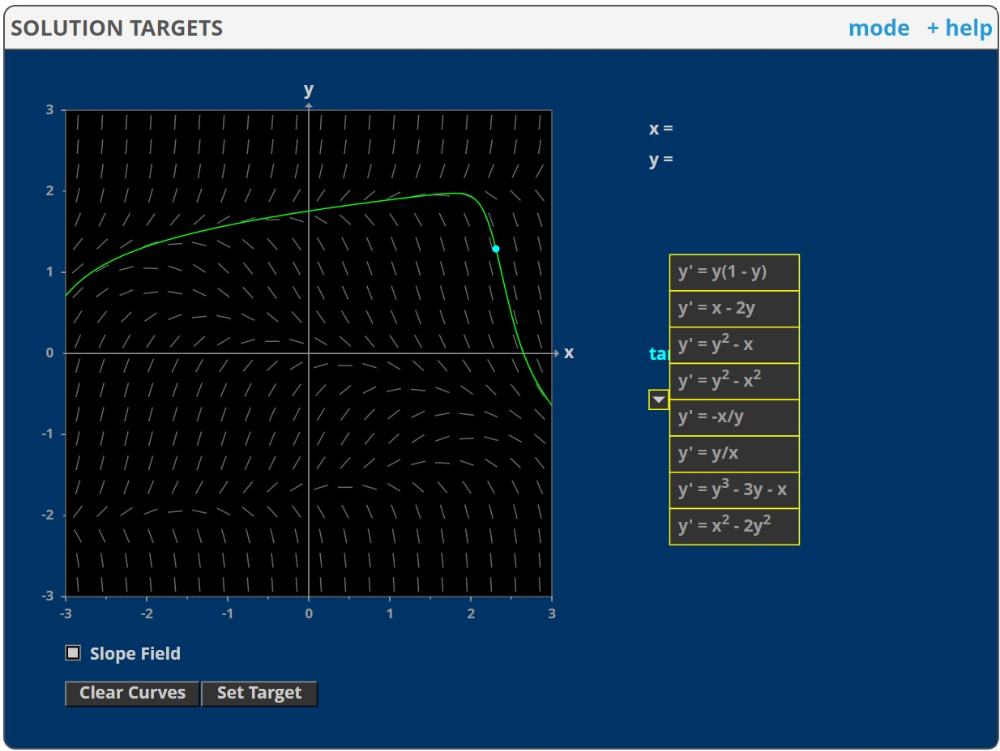
Undersöka 1:a ordningens differentialekvationer med hjälp av riktningsfält

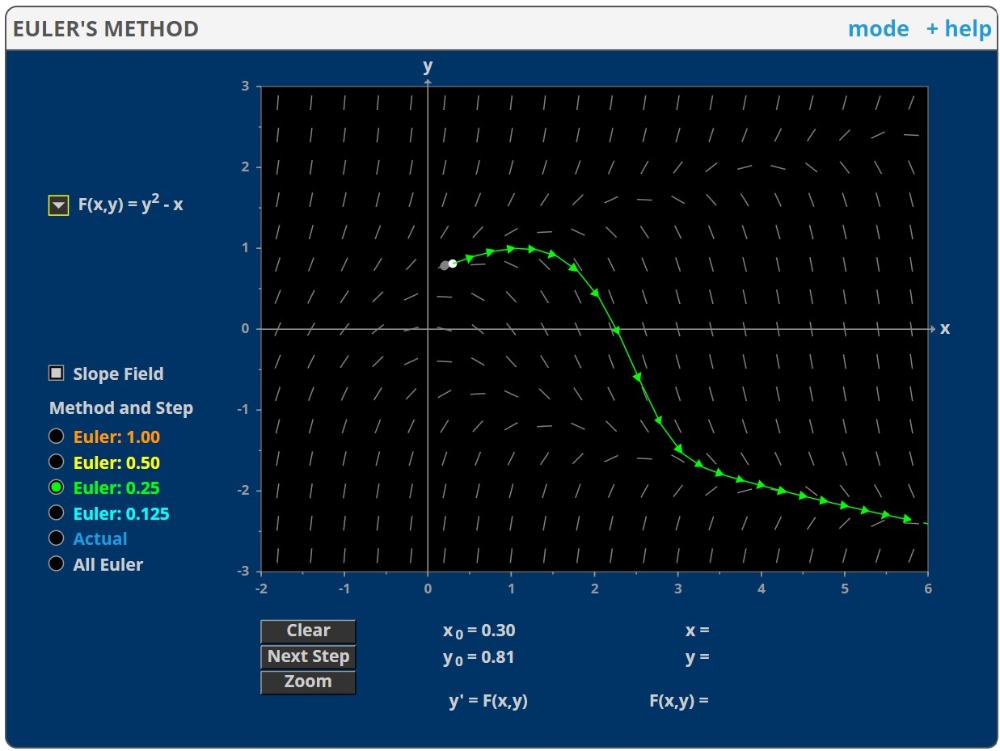
Eulers metod demonstreras för ett antal givna 1: a ordningens differentialekvationer av formen
dy/dt=f(t,y)

Du väljer stegländen  (från ett antal givna), och sedan kan du stegvis få fram lösningskurvan samt tabell. Riktningsfältet är upprittad, och den exakta lösningen kan visas så att du kan se noggranheten på metoden.

 

Flera simuleringar från samma sida 

Nya HTML5 simuleringar, som funkar med alla webbläsare, Startsidan finns HÄR  (Välj: Open DME for students).

Logga in som gäst och klicka exempelvis:

Higher education -> Differential equations

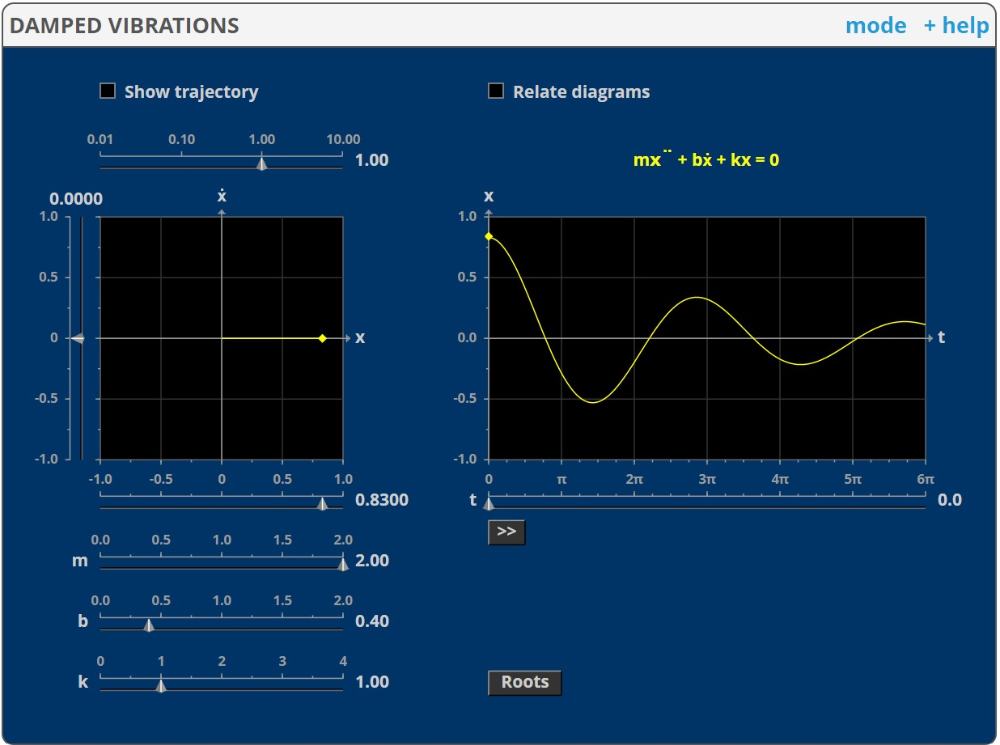
En kropp med massan m svänger kring sitt jämviktsläge. Den påverkas dels av en återförande kraft från fjädern:
-k·x, där k är fjäderkonstanten och x avståndet från jämviktsläget; och dels av en dämpad (friktions) kraft som är proportionell mot hastigheten: -b·x’.

Newtons andra lag (F=ma=mx’’) ger differentialekvationen:
m·x’’+b·x’+k·x=0

Simuleringen undersöker denna ekvation. Du kan välja olika värden på variablerna, och begynnelsevillkoren (x och x’’ vid t=0) väljs i fönstret till vänster. När du trycker på "»", så visas en animering av rörelsen.  

 

Flera simuleringar från samma sida

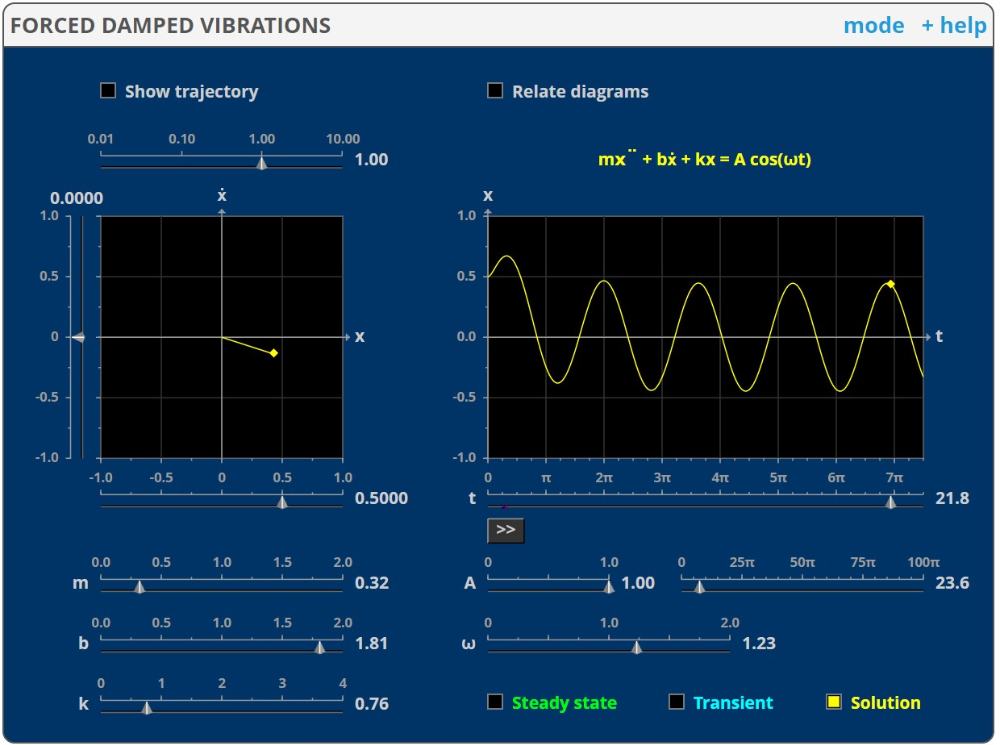
En kropp med massan m svänger kring sitt jämviktsläge. Den påverkas av tre krafter. En återförande kraft från fjädern: -k·x, där k är fjäderkonstanten och x avståndet från jämviktsläget; en dämpad (friktions) kraft som är proportionell mot hastigheten: -b·x’ ; och en yttre påtvingad kraft: A·cos(ωt).

Newtons andra lag (F=ma=mx’’) ger differentialekvationen:
m·x’’+b·x’+k·x=A·cos(ωt)

Simuleringen undersöker denna ekvation. Du kan välja olika värden på variablerna, och begynnelsevillkoren  (x och x’’ vid t=0) väljs i fönstret till vänster. När du trycker på "»", så visas en animering av rörelsen.

Du kan välja att visa den homogena lösningen ("Transient" =övergående; eftersom den homogena lösningen har en dämpningsfaktor e^-r·t där r >0 och därmed bli liten när t är stort), den partikulära ("Steady State" eftersom det är den som blir kvar efter lång tid) eller den exakta lösningen. 

 

Flera simuleringar från samma sida

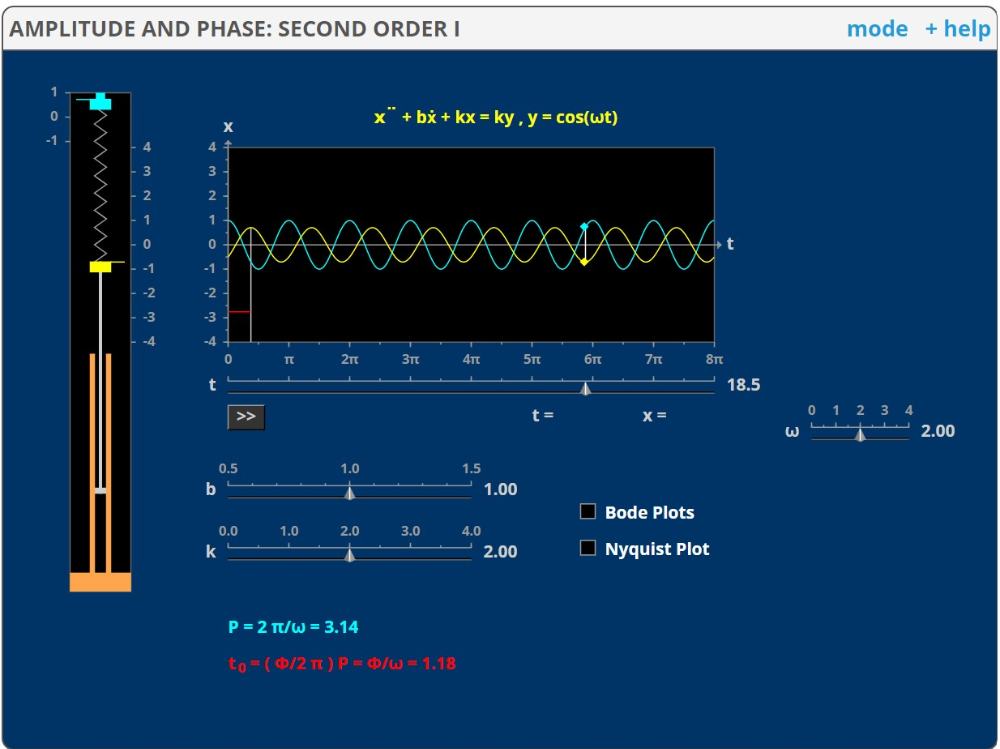
En kropp med massan m=1kg svänger kring sitt jämviktsläge. Den påverkas av tre krafter. En återförande kraft från fjädern: -k·x, där k är fjäderkonstanten och x avståndet från jämviktsläget; en dämpad (friktions) kraft som är proportionell mot hastigheten: -b·x’ (nedre delen av uppställningen); och en yttre påtvingad kraft genom att fjäderns hängpunkt svänger enligt h(t)=cos(ωt). Detta resulterar till en påtvingad kraft: k·h(t)= k·cos(ωt). 

Newtons andra lag (F=ma=mx’’) ger differentialekvationen:
m·x’’+b·x’+k·x=k·cos(ωt)

Simuleringen undersöker den partikulära lösningen
P(t)=c·cos(ωt)+d·sin(ωt)= A·cos(ωt+φ)
(Efter lång tid dör den homogena lösningen ut eftersom den har en dämpningsfaktor:
e^-rt, och kvar blir bara den partkulära lösningen). 

I fönstren längst upp till höger visas A och φ som funktion av ω. Det intressanta är att vid ett visst värde på ω_A=√(k/m-b²/2m²) så ökar amplituden A kraftigt. Vi har fått en resonans. Ju mindre dämpningsfaktorn b är desto mera påtagligt blir resonansfenomenet.

Du kan välja olika värden på variablerna b, k och ω. När du trycker på "»", så visas en animering av rörelsen.  

 

Flera simuleringar från samma sida