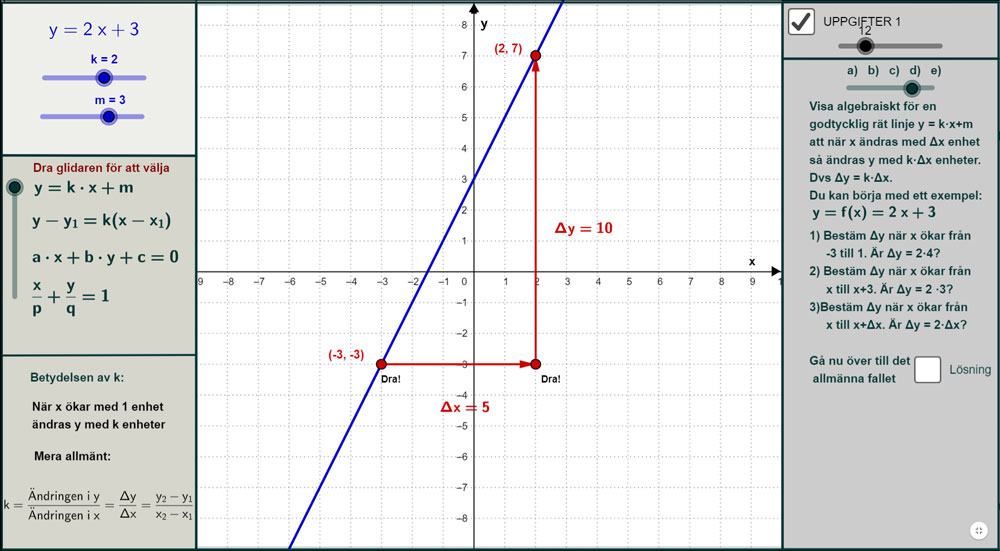
Ma1: Du kan undersöka den linjära funktionen i k-form
Ma2: Du kan undersöka den linjära funktionen i k-form enpunkts- och tvåpunktsform, samt allmän form.
Det finns många olika typer av uppgifter (undersökande, utredande, laborativa mm) integrerade i simuleringen. Stegvis hjälp och lösningar finns till varje uppgift.
Skapat med GeoGebra av Georgios Theodoridis
Starta med en figur i 4:e kvadranten. Spegla den först i x-axeln och sedan i y-axeln. Vilka symmetrier har den resulterande figuren?
Georgios Theodoridis, Skapat med GeoGebra
Undersöka andragradsfunktioner i olika former
Skapat med GeoGebra av Georgios Theodoridis
Heltäckande sammanfattning av Ma 3c med teori och lösta uppgifter i alla moment.
Texten kan exempelvis användas inför ett prov i Ma 3c eller som en repetition av kursen inför Ma 4.
HTML5 Geometri: Teori och övningar för sin v, cos v och tan v
Georgios Theodoridis. Skapat med GeoGebra
Tallinjen kan undersökas. Du kan också välja att undersöka tre olika betydelser av minustecknet.
Skapat med GeoGebra av Georgios Theodoridis
HTML5 Version 2: Vinkelmått och derivatan av y = sin x
Skapat med GeoGebra av Georgios Theodoridis