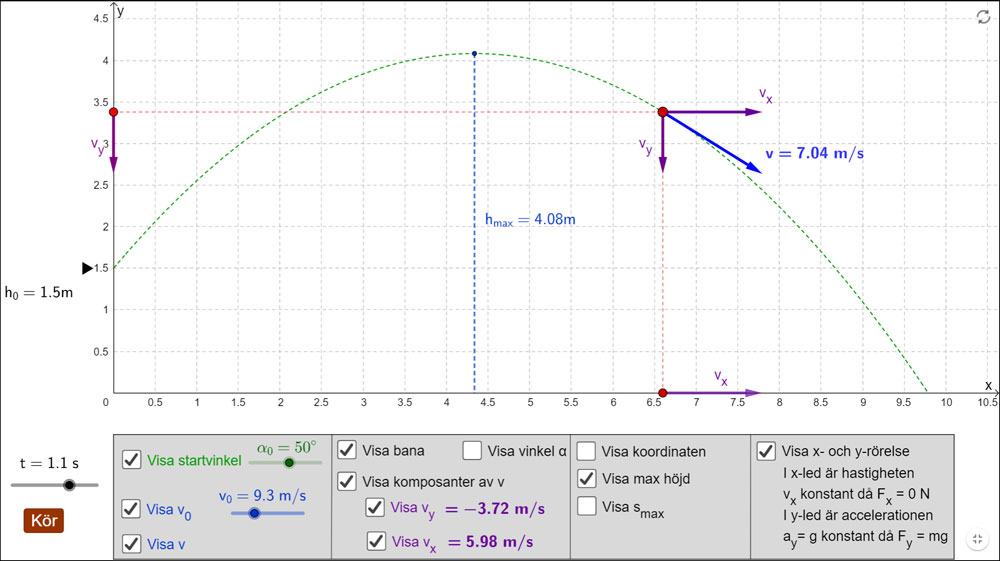
Kaströrelsen från olika höjder kan undersökas.

Skapad med GeoGebra av Georgios Theodoridis

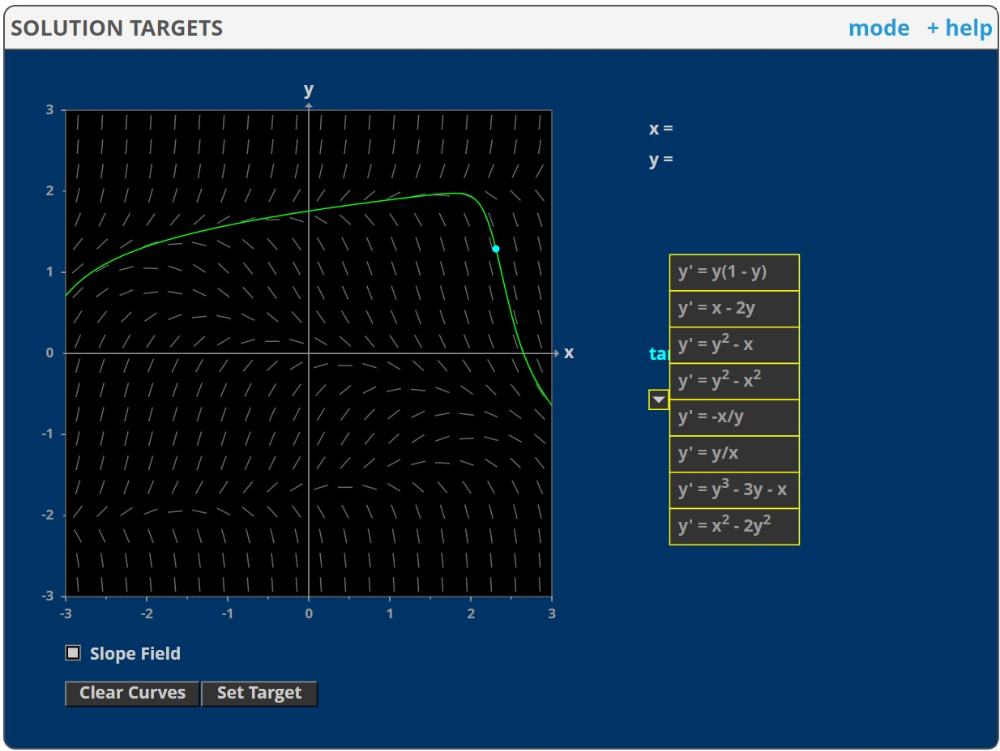
Undersöka 1:a ordningens differentialekvationer med hjälp av riktningsfält

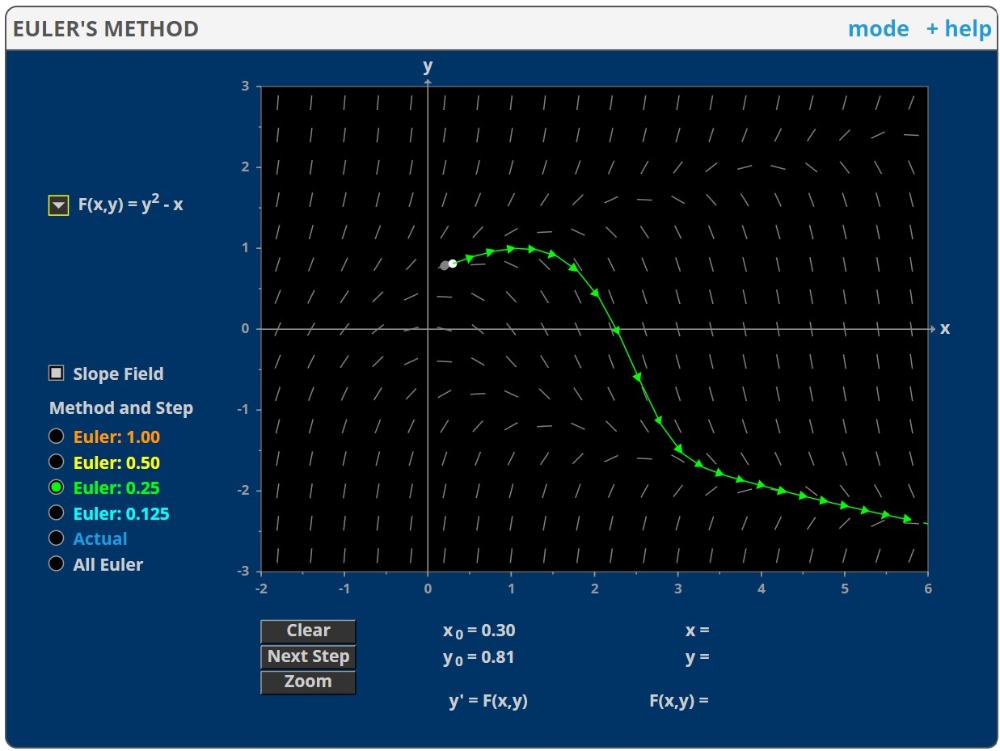
Eulers metod demonstreras för ett antal givna 1: a ordningens differentialekvationer av formen
dy/dt=f(t,y)

Du väljer stegländen  (från ett antal givna), och sedan kan du stegvis få fram lösningskurvan samt tabell. Riktningsfältet är upprittad, och den exakta lösningen kan visas så att du kan se noggranheten på metoden.

 

Flera simuleringar från samma sida 

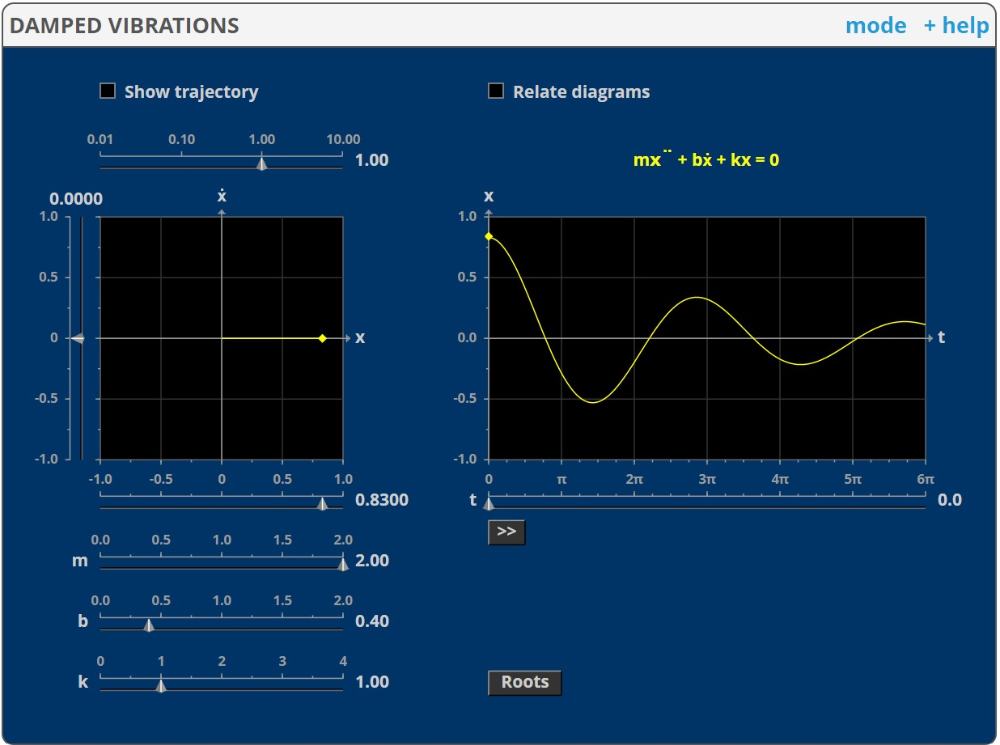
En kropp med massan m svänger kring sitt jämviktsläge. Den påverkas dels av en återförande kraft från fjädern:
-k·x, där k är fjäderkonstanten och x avståndet från jämviktsläget; och dels av en dämpad (friktions) kraft som är proportionell mot hastigheten: -b·x’.

Newtons andra lag (F=ma=mx’’) ger differentialekvationen:
m·x’’+b·x’+k·x=0

Simuleringen undersöker denna ekvation. Du kan välja olika värden på variablerna, och begynnelsevillkoren (x och x’’ vid t=0) väljs i fönstret till vänster. När du trycker på "»", så visas en animering av rörelsen.  

 

Flera simuleringar från samma sida