Dämpad svängning
En kropp med massan m svänger kring sitt jämviktsläge. Den påverkas dels av en återförande kraft från fjädern:
-k·x, där k är fjäderkonstanten och x avståndet från jämviktsläget; och dels av en dämpad (friktions) kraft som är proportionell mot hastigheten: -b·x’.
Newtons andra lag (F=ma=mx’’) ger differentialekvationen:
m·x’’+b·x’+k·x=0
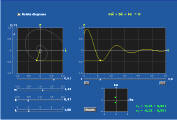
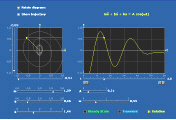
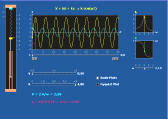
Simuleringen undersöker denna ekvation. Du kan välja olika värden på variablerna, och begynnelsevillkoren (x och x’’ vid t=0) väljs i fönstret till vänster. När du trycker på "»", så visas en animering av rörelsen.